实验原理
考虑一根长为![]() ,直径为
,直径为![]() (
(![]() )的长细棒,取其轴线方向为
)的长细棒,取其轴线方向为![]() 轴,则其振动方程为
轴,则其振动方程为
![]() (1)
(1)
长棒沿![]() 方向振动,
方向振动,![]() 指长棒
指长棒![]() 处截面在
处截面在![]() 时刻的
时刻的![]() 方向位移。
方向位移。![]() 为试棒的杨氏模量,
为试棒的杨氏模量,![]() 为材料密度,
为材料密度,![]() 为棒的横截面积,
为棒的横截面积,![]() 为其截面的惯量矩。
为其截面的惯量矩。
![]() (2)
(2)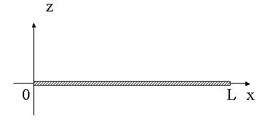
图1 长棒沿![]() 方向振动
方向振动
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
式中,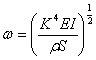 (6)
(6)
(5)式称为频率公式。由式可看出,若已知频率等其它条件,可算出杨氏模量。
如果支撑点在试棒的节点,即处于共振状态的棒中,位移恒为零的位置附近(如图2图3中的节点位置),则棒的两端均处于自由状态,此时的边界条件为:两端横向作用力和弯矩均为零,所以
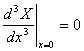 ,
,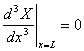 ,
,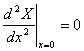 ,
,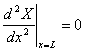 (7)
(7)
由此可解得
![]() (8)
(8)
用数值解法求得本征值![]() 和棒长
和棒长![]() 应满足
应满足
![]() ,4.730,7.853,10.996,14.137,…… (9)
,4.730,7.853,10.996,14.137,…… (9)
其中![]() 的根,对应于静止状态,因此将
的根,对应于静止状态,因此将![]() 记做第一个根,对应的振动频率称为基振频率,此时棒的振幅分布如图2-3-2所示。而图2-3-3曲线对应于
记做第一个根,对应的振动频率称为基振频率,此时棒的振幅分布如图2-3-2所示。而图2-3-3曲线对应于![]() ,称为一次谐波。将第一个本征值
,称为一次谐波。将第一个本征值![]() 代入4-2-6式,可以得到自由振动的固有频率
代入4-2-6式,可以得到自由振动的固有频率
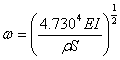 , (10)
, (10)
解得该金属棒的杨氏模量为:![]() (11)
(11)
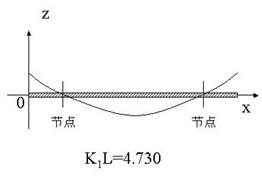
图2 基振频率时棒的振幅分布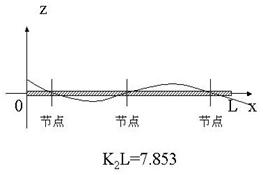
图3 一次谐波时棒的振幅分布
对于直径为![]() 的圆棒,其惯量矩
的圆棒,其惯量矩![]() ,代入11式得
,代入11式得
![]() (12)
(12)
f为频率。在实际测量中,由于不能满足![]() ,所以上式应乘以一个修正系数
,所以上式应乘以一个修正系数![]() ,即
,即
![]() (13)
(13)
![]() 可根据
可根据![]() 的不同数值和材料的泊松比查表得到钢棒的修正系数表
的不同数值和材料的泊松比查表得到钢棒的修正系数表
