1. 布拉格公式

x射线投射到晶体上时，除了要引起晶体表面平面点阵的散射外，还要引起晶体内部平面点阵的散射，全部散射线相互干涉后产生衍射条纹如图1。

 

 

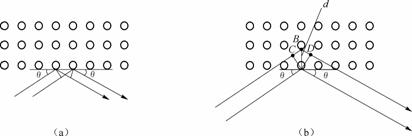
图1晶体散射

设相邻散射平面点阵的间距为d，则从两相邻平面点阵散射出来的x 射线之间出来的光程差为BC+BD=2d.sinq，所以相干加强的条件为：

此式即为布拉格衍射公式。式中l为X射线的波长，q为掠射角（投射线与晶面之间的夹角），k为干涉级数。它也是我们的微波布拉格衍射实验的基本公式。

2. 晶体平面族（晶面族）

晶体点阵上的格点，按一定的对称规律周期地重复排列在空间三个方向上。因此晶体的立体点阵可以用一系列间距相等的平行晶面来表示。布拉格公式中的d值就是这样的晶面族中相邻两晶面的间距。晶体点阵中的平行晶面族有许多种取法，每种取法有着特定的晶面法线方向。晶面法线方向的矢量代表着晶面的取向。图32-3就画出了二维点阵中一些晶面族的取法。

对于特定取向的晶面，我们采用密勒指数h、k、l（三个互质的整数）来表示，称为晶面的密勒指数，该平面族就称为（hkl）晶面族。

  例如，某平面在三个坐标轴上的截距分别为x=3,y=4,z=2（见图2(a)）,取倒数再化做互质的整数即：

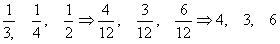
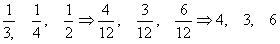
所以此平面的密勒指数为(436)，即此平面的平行晶面族记为（436）。

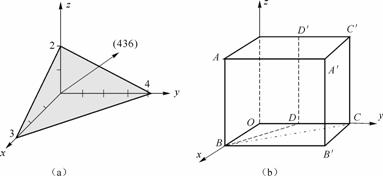
图2 用密勒指数表示平面

又如图2(b)所示，平面ABB′A′在三个坐标轴上的截距为x=1,y=￥,z=￥，所以密勒指数为（100）。ABC C′ 平面的截距为x=1,y=1,z=￥的，所以密勒指数为（110）。依次类推，平面ABDD’的密勒指数为(120)。

我们略去晶胞的空间结构，俯视图2(b)所示的点阵，可得立方晶体在x-y平面上的投影如图3所示。实线表示（100）平面与x-y平面的交线，点划线与虚线分别表示（110）面及（120）面与x-y平面的交线。其它晶面族密勒指数依法类推。对于立方晶系，d100=d010=d001=d，可以证明各晶面族的面间距计算公式为：

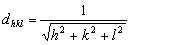
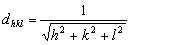
3. 模拟立方晶体晶面族的微波布拉格衍射

如图3所示，今有一束平行的微波入射（100）平面族，根据x射线的布拉格衍射公式，全部散射线相互干涉加强条件为：

 

 

若实验测得掠射角q，则从已知的微波波长l可求晶面族间距d100。反之若知晶面族的间距，可求微波的波长。对于其它晶面族，全部散射线相互加强条件依次类推。

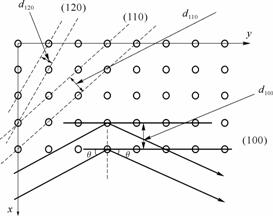
图3 二维晶面