一、双棱镜的干涉

双棱镜实验是继杨氏双缝实验后菲涅耳提出的一种利用双棱镜获得两相干光束而形成干涉的方法，可以在简单的情况下观测到双光束干涉产生的干涉条纹。

双光束干涉原理

双棱镜能将一个光源分成两个相干光源的分光元件。双棱镜是由玻璃制成的等腰三角棱镜，两棱角为很小的锐角，顶角为很大的钝角。利用双棱镜的折射作用，可以使照射到双棱镜上的一束光分成传播方向不同的两束光。由点光源S发出的光经双棱镜折射后，分为两束如同是从虚光源S₁和S₂发出的相干光束，并使之在传播时有一部分彼此重叠形成干涉。若在两束光叠加区域内设置观察屏，则屏上会出现明暗相间的干涉条纹。相干叠加的光强分布为

其中，Δφ为两光源S₁和S₂发出的两光波到达相遇处的相位差，Δ为相应的光程差，     为波长。

双棱镜干涉光强分布

屏上条纹的位置

条纹间距

   由于两束光叠加的区域比较窄，干涉条纹的间距很小，所以双棱镜干涉一般要借助于仪器来观测。如果将观察屏放在较远的地方，用眼睛就可以看到屏上清晰的明暗相间的干涉条纹。

二、夫琅和费衍射

衍射物与光源和接收屏的距离都是无穷远时的衍射为夫琅和费衍射。

一般衍射物与接收屏的距离

即可视为夫琅和费衍射，式中的a为缝宽。在实验室条件下，用激光作为光源，将观察屏（或光电探测器）放在较远处，就可以满足夫琅和费衍射的远场条件。

 (一) 缝的衍射

1.    单缝衍射

单缝衍射示意图

夫琅和费单缝衍射光强分布规律为

根据光强分布规律：

（1）u=0 , 即衍射角θ=0时，P处的光强I=I₀为最大值，称中央主极大。

（2）u=kπ, 即衍射角θ满足

时，I=0为极小值，即P处出现暗纹。k为级次。θ角很小，第k级暗纹所对应的衍射角可表示为

（3）k=±1时，中央主极大两侧暗纹间的角宽度(中央亮纹的角宽度)为

其他任意相邻暗纹间的角宽度为

2.   双缝衍射

   对衍射物是两个缝的宽均为a，中间不透光部分的宽度为b的双缝，一般将a+b称为双缝的缝距。夫琅和费双缝衍射的光强分布规律为

其中：

双缝与接收屏的距离为L时，其相邻亮纹（或暗纹）的间隔  

夫琅和费双缝衍射可以看作缝宽为a的单缝衍射光强调制下的双光束干涉。两个因子中，只要有一个为零，合光强则为零。  

干涉极大若出现在衍射极小的位置上时，合光强为零，干涉极大消失，出现缺级现象：缺级发生在

(其中j= 1,2,3,…，) 的级次上。

点击“单缝”，“双缝”和“合成”观察不同情况下光强分布的变化情况

3.    多缝衍射

当衍射物是N条狭缝的宽均为a，中间不透光部分的宽度为b的多缝时，夫琅和费N缝衍射的光强分布公式

其中：

夫琅和费N缝衍射的相对光强是宽度为a的单缝夫琅和费衍射与N个相干光束干涉光强的乘积。当v=kπ即

时，产生干涉主极大的亮条纹。相邻的主极大的间隔

相邻的主极大亮纹之间有N- 1条暗纹。相邻暗纹之间有一个次极大，即相邻的主极大之间有N– 2个次极大。缺级出现在(a+b)/a为整数的级次上。

夫琅和费多缝衍射：单缝衍射调制的多光束干涉。

点击“单缝”，“多缝”和“合成”观察不同情况下光强分布的变化情况

4.光栅：

狭缝的数目增加时，衍射图样的主极大亮条纹变细变亮，次极大数目增多，光强减弱。平行、等宽且等间距的多狭缝称为光栅。

(二)孔的衍射

1．矩孔衍射

矩孔的边长分别为a₁和a₂时，夫琅和费矩孔衍射的光强分布公式为

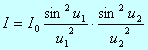
其中：

，

I₀是衍射场中心光强。

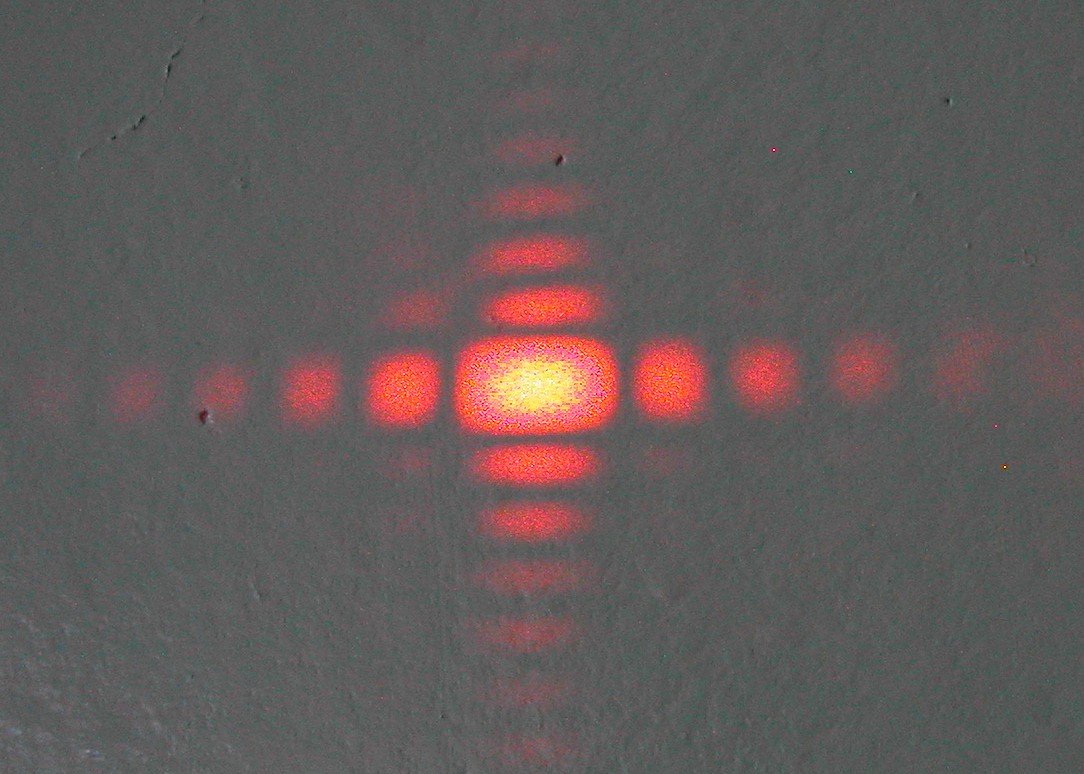
矩孔衍射图

2．圆孔衍射

直径为D的圆孔的夫琅和费衍射光强的径向分布可通过贝塞耳函数表示。

夫琅和费圆孔衍射图样的中央圆形（零级衍射）亮斑通常称为艾里斑，艾里斑的大小可用半角宽度即第一级暗环对应的衍射角为：

圆孔衍射各极小值的位置在u= 0.610π，1.116π，1.619π，…处；各极大值的位置在u= 0，0.0819π，0.133π，0.187π，…处，其相对光强I/I₀依次为1，0.0175，0.042，0.0016，…。零级衍射的圆亮斑集中了衍射光能量的83.8% 。

3．双圆孔衍射

每个孔产生小孔衍射，两个圆孔的光波之间产生干涉。因此夫琅和费双圆孔衍射即为圆孔衍射调制的双光束干涉。

双圆孔衍射图