非线性科学和复杂系统的研究是二十一世纪科学研究的一个重要方向。非线性科学的研究对了解生物，物理，化学，气象等学科都有着十分重要的意义。近20多年来，混沌作为非线性科学中的主要研究对象之一，在许多领域都得到证实和应用。作为一门新学科，混沌填补着自然界决定论和概率论的鸿沟。混沌是对经典决定论的否定，但本身有它特有的规律。研究混沌的目的是要揭示貌似随机的现象背后所隐藏的规律。

人们在认识混沌之前，一直认为力学系统服从确定的规律，即当初始条件确定后，力学系统将按确定的轨道运动，从而人们可以对系统的运动作出预言。然而伟大的法国数学家，物理学家—庞加莱在研究天体力学，特别是在研究三体问题时发现了混沌。他发现三体引力相互作用能产生惊人的复杂行为，确定性动力学方程的某些解有不可预见性。在《科学的价值》一书中写道：“初始条件的微小差别在最后的现象中产生了极大的差别；前者的微小误差促成了后者的巨大误差，于是预言变的不可能了”。这些描述实际上已经蕴涵了“确定性系统具有内在的随机性”这一混沌现象的重要特征。

美丽的混沌图像

1963年，混沌学研究有了另一个重大突破。美国气象学家洛仑兹（Lorenz E）发现了大气变化的非周期性。洛仑兹虽是从事天气预报工作的气象学家，但数学功底十分扎实。在五、六十年代，人们普遍认为气象系统虽然非常复杂，但仍然是遵循牛顿定律的确定性对象，在有了计算机后，天气状况可以改变和控制。当时，洛仑兹将大气对流模型用计算机做数值计算 ，观察这个系统的演化行为。在计算观察中，看到了这个确定性系统的有规则行为，同时也发现了同一系统在某些条件下出现非周期的无规则行为---蝴蝶效应。洛仑兹揭示了一系列混沌运动的基本特征，如确定性非周期性、对初值的敏感性、长期行为的不可预测性等，他还在混沌研究中发现了第一个奇异吸引子---洛仑兹吸引子，为混沌的研究提供了一个重要模型。

点击这里观看洛仑兹吸引子

观看授课录像

混沌运动最主要的特征是具有初值敏感性和长时间发展趋势的不可预见性。混沌研究表明：一个完全确定的系统，即使非常简单，由于系统内部的非线性作用，同样具有内在的随机性，可以产生随机性的非周期运动——混沌。在许多非线性动力学系统中，既有周期运动，又有混沌运动。混沌运动不是由外噪声引起的，而是非线性方程所特有的一种解；混沌吸引子是由确定性方程中非线性因数直接得到的具有随机性运动的一种状态。本实验通过一个简单的电路产生混沌，讨论倍周期分叉产生混沌的过程，同时了解非线性电阻对产生混沌的作用，并了解混沌现象的一些基本特征。

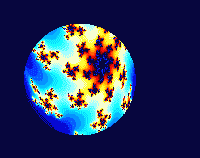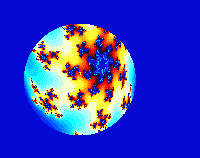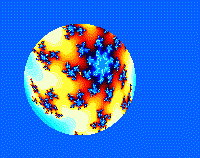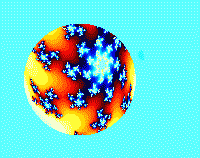
这里展示了分形的过程，分形是史研究混沌的方法之一